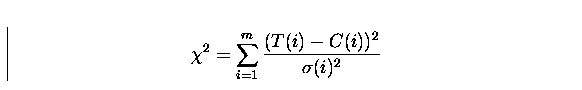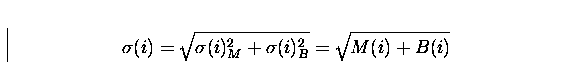Next: Response in the GRBM
Up: Response matrix and spectral
Previous: Building the response matrix
If we indicate with R(i,j) the generic element of the response matrix, i.e. the
probability that an incoming photon with energy comprised in the range of
input energy channel j gives a count in the PHA channel i, and F(E)
the incident photon flux giving the number of incoming photons for each
response matrix input energy range j, the corresponding expected value of the number of counts in
the channel i is given by:
| 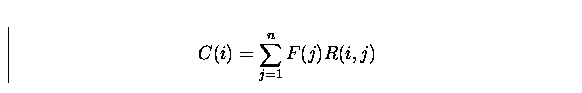 |
(10) |
, where n is the number of the response matrix input energy bins and
| 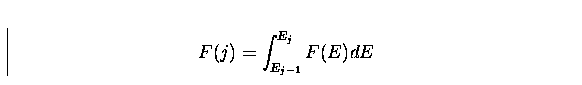 |
(11) |
, Ej-1 and Ej being the energy bounds of the response matrix
input energy channel j.
Conventionally, F(E) is expressed in photons cm-2 s-1 keV-1,
R(i,j) in cm2 (i.e. in terms of effective area) and C(i) in
counts s-1 channel-1.
As we have discussed, the response matrix R is not diagonal, and thus it
cannot be inverted to directly extrapolate the incident photon spectrum
F(E) from the measured spectrum C. In other words, this means that
different incident photon spectra F(J) may result in the same value of
C(I). The standard technique adopted to analyze spectral data of hard X-ray
and gamma-ray experiments is the spectral fitting, which consists
in assuming a parametrical photon spectrum model M(E,P1,...,Pn), integrate
it in each response matrix input energy bin as in eq. 3.11 to obtain
M(j,P1,...,Pn), generate
a theoretical count spectrum T(i) by using equation 3.10 replacing
F(j) with M(j), compute the value of 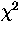 as:
as:
| 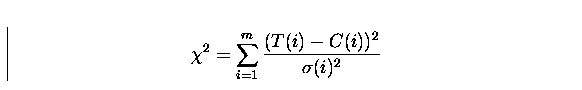 |
(12) |
, where 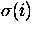 is the standard deviation of C(i) and m the number of
PHA channels,
find the parameter values which minimize the
is the standard deviation of C(i) and m the number of
PHA channels,
find the parameter values which minimize the 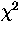 and test the
goodness of the fit by means of the
and test the
goodness of the fit by means of the 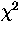 test.
test.
To perform the 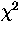 minimization and find the best fit parameters,
together with associated errors, for a given model standard software packages
are used, like XSPEC ([NASA/HEASARC]), developed at HEASARC, or MINUIT ([James 1994])
developed at CERN. It is important to stress that more than one model
may fit well the measured spectrum; the choice between models can be done
basing on statistical tools (like the F-Test) and/or on scientific
interpretation.
minimization and find the best fit parameters,
together with associated errors, for a given model standard software packages
are used, like XSPEC ([NASA/HEASARC]), developed at HEASARC, or MINUIT ([James 1994])
developed at CERN. It is important to stress that more than one model
may fit well the measured spectrum; the choice between models can be done
basing on statistical tools (like the F-Test) and/or on scientific
interpretation.
It is important to note that C(i) is not measured directly, because
the actually measured spectrum is the sum of
the background plus the source spectrum, and thus it is calculated as:
, where M(i) is the measured spectrum and B(i) the background spectrum.
The error 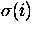 is then given by:
is then given by:
| 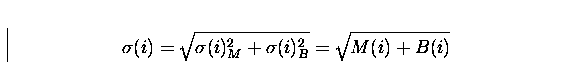 |
(14) |
, because M(i) and B(i) are Poissonian distributed and thus their standard
deviation is equal to their mean value.
Finally, the 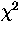 statistics can be used to test the model hypothesis only
if the number of counts in each channel C(i) is greater than about 20, so
that its distribution can be assumed Gaussian. Therefore, in case of weak
signals, the PHA channels are grouped in order to have a measured spectrum
with at least 20 counts in each channel. test must be adopted, e.g. the C test.
statistics can be used to test the model hypothesis only
if the number of counts in each channel C(i) is greater than about 20, so
that its distribution can be assumed Gaussian. Therefore, in case of weak
signals, the PHA channels are grouped in order to have a measured spectrum
with at least 20 counts in each channel. test must be adopted, e.g. the C test.




Next: Response in the GRBM
Up: Response matrix and spectral
Previous: Building the response matrix
Lorenzo Amati
8/30/1999
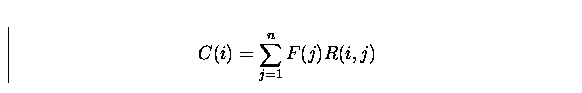
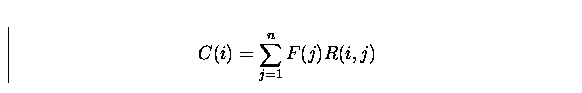
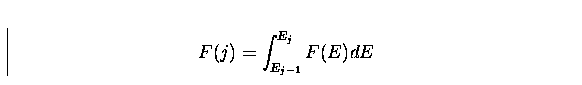
![]() as:
as: