Building the response matrix

As discussed above, the final step in the measurement of the incident photon energy by a scintillator counter (but this is true for all X-and gamma-ray astronomical detectors) is the Pulse Height Analysis performed by the electronics, which assigns the processed signal to a PHA value. Thus, the final measured spectrum of a source in a given exposure time is in the form of an histogram containing the number of counts for each PHA channel. To extract information on the spectrum of the source, one must know and describe in some useful mathematical form the following fundamental information on the instrument's response:

• Efficiency: this is the ratio between the number of measured counts and the number of incident photons for a radiation beam of given energy and from a given direction. It gives the probability that the photon will interact and deposit all or part of its energy into the crystal. Detectors efficiency depends on the physical and geometrical properties of the detector, of the materials constituting its entrance window and the surrounding environment, and thus on the interaction mechanisms of gamma-rays with matter described in the previous section. It is usually expressed in terms of effective area, in cm², corresponding to the geometrical area of an ideal detector with unit efficiency and which would measure the same number of events. Thus it can be expressed as:

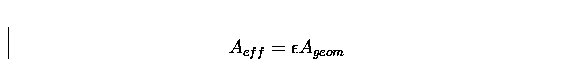  $$A_{eff}=\epsilon A_{geom}$$ (9)

  , where A_eff is the effective area, 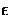$\epsilon$ the efficiency and A_geom the geometrical area;
• Response function: the detector response function gives the probability that a photon of energy E undergoing an interaction into the detector will be measured as a count at an energy E' in the measured spectrum. Thus, the response function contains all the information on energy deposition in the crystal (the physics of the interaction of gamma-rays with the detector) and on crystal and PMT response (i.e. the energy resolution factors). Given the complexity of gamma-ray spectra, the determination of the response function is very complex. Usually (e.g. [Band et al. 1992]), its reconstruction is practically divided in two main tasks: a) the estimation, by means of Monte Carlo simulations, analytical calculations and experimental measurements (e.g. [Pendleton et al. 1995]), of the probability that the photon interacts with the detector (thus including efficiency modeling), that a given type of interaction takes place and of the relative energy loss distribution; b) estimation of the energy resolution as a function of photon energy and interaction placement in the detector by means of experimental measurements of monochromatic sources photo-peaks characteristics and the analytical modeling of crystal, PMT and electronic behaviors;
• Channel to energy conversion: as we have discussed in previous section, the physics of the interaction of gamma-ray with the detector and the finite detector energy resolution cause the fact that for a given incident photon energy different final PMT pulse amplitudes can be generated. Thus, the PHA channels do not correspond to a single photon energy. Conventionally, the energy range of a PHA channel is identified with the energy range of incident photons whose photo-peaks centroid in the PHA spectrum fall within the channel. The effective values of channels energy bounds are determined by means of on-ground calibrations with monochromatic sources, as will be described below for the GRBM. For an ideal detector, there would be a linear and stable relationship between the centroid of the photo-peak corresponding to each incident photon energy and the final PMT output pulse amplitude. In practice, different factors, the most common of which are changes in the light yield of the scintillator and in PMT gain can alter significantly the energy to channel relationship. The determination of the effective energy bound of each channel is performed by means of on-ground calibrations with monochromatic sources, as will be described below for the GRBM, and the in-flight stability of the energy to channel conversion can be monitored and adjusted by automatic gain control techniques (as for the PDS main detectors) or the use of gain calibration sources (as for the GRBM detectors);
• Thresholds effects: to better delimitate the energy band of the detector, or to divide it into different ranges (as e.g. for BATSE), discriminator circuits in the associated electronics are used. The discrimination is based on PMT pulse amplitude, and thus the upper and lower thresholds nominal energy values do not correspond to incoming photon energies, depending on energy deposition mechanisms and instrument finite resolution. At low energies, photo-electric absorption occurs for most of the photons interacting with the crystal; thus, the cut-off in the detector' s band is close to the nominal energy of the threshold, with uncertainties due to the finite energy resolution which can cause photons with energies below the energy threshold to generate final pulses with amplitude above it. At high energies, i.e. when Compton scattering is the main interacting mechanism, in addition to the energy resolution effect, it can happen that photons with energies even much higher than that of the threshold deposit in the detector an energy below it. In other words, the effect of thresholds on the measured spectrum of a monochromatic source of high energy photons (say above 200 keV), will be to exclude the photo-peak (or a portion of it if photons energy is close to the threshold) and to generate a cut-off in the Compton continuum. Other threshold effects on the detector response include the change of the threshold energy value, due to changes in PMT gain or change in crystal light response, and the non perfect threshold cut-off due to the electronics.

These are the 'ingredients' needed for the construction of the detector response matrix, which is the conventional and practical form in which the detector response is expressed. The response matrix is a bi-dimensional matrix in which each element is the probability that an incoming photon with energy belonging to a given energy range will be assigned to a given PHA channel. The width and number of the ranges (or channels) in which the energy of the incoming photons is divided depends on the instrument energy resolution (i.e. 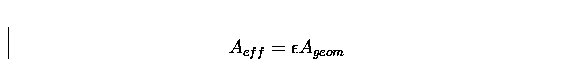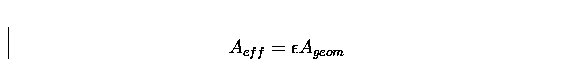at energies greater than $\sim$ 20 keV a channel width of 1 keV oversamples detector's resolution) and the complexity and the dependency on energy of the response function. In principle, the incoming photon energy range should go from 0 to infinite, but in practice, it is determined on the basis of the window transparency, detector efficiency and electronics thresholds. At low energies, where almost all the absorption is through the photo-electric process , it is possible to estimate a photon energy below which the photons will not be detected by the instrument. The estimation of the upper limit of the detectable photon energy range is much more complex, because the response matrix is not diagonal, Compton scattering preveals and the energy deposited in the detector can be much less than the incoming photon energy, thus bypassing the high energy threshold, if any. Nevertheless, crystal total absorption coefficient goes down with increasing photon energy, reaching, e.g. for CsI, a minimum around 2000 keV, where pair production becomes the main absorption mechanism. Accounting for this and for the effect of the eventual high energy threshold, it is possible to estimate an energy such that photons with energies above it have negligible probabilities of being detected or at least to evaluate the flux with the help of some auxiliary assumptions on the source.