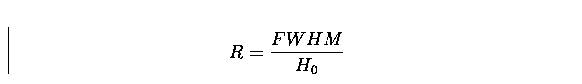Next: Response matrix and spectral
Up: Gamma-ray spectroscopy with inorganic
Previous: Interaction of gamma radiation
In the ideal detector assumption made above, the resulting measured spectrum of
a gamma-ray source with photons energy ranging e.g. from 20 to 2000 keV, would be the sum of the individual components relative to the different absorption mechanisms illustrated in Fig. 3.2. In real inorganic scintillator detectors the
response function is complicated and distorted by different factors, that have
to be taken in consideration; we describe below the most common and of interest
for GRBM response reconstruction.
Effects due to geometry and size of the detector
For photons
absorbed via photo-electric effect near the crystal surface, it may happen that
the fluorescence photon escapes the detector without
being re-absorbed. In this case the energy deposited in the detector is less
than the incident photon energy, and this class of events forms a new peak called escape peak at an energy equal to the the photon energy minus the
characteristic X-ray photons. This feature is important and evident in gamma-ray spectra of photons with energy less than about 100 keV and materials with high Z (the probability of emission of an X-ray characteristic photon with respect to that of an Auger electron increases with Z and decreases with photon energy) in detectors
with high values of the surface to volume ratio (like the GRBM). Moreover, if the detector is sufficiently large and thick, photons
interacting with the crystal via Compton scattering may undergo more than one
single scatter, thus depositing an energy greater than that predicted by eq.
2.2., and possibly greater than the maximum energy represented by the Compton edge. The result in the observed spectrum is a distortion of the Compton continuum shape filling of the gap between the Compton edge and the photo-peak.
These events are called multiple scattering events. Finally, in the case of pair production, one or both the generated electron and positron may escape
the detector, resulting in a rather complex spectrum ([Knoll 1989,Siegbahn 1966]). Other effects which
become important for photon energies above few MeV (thus of less interest for
the GRBM response) include secondary electron escape and bremsstrahlung escape.
Surrounding material and environmental effects
In real detecting system, an important contribution to the measured spectrum
of the source may be due to photons generated by the interaction of source photons with the surrounding materials and creating photons of lower energy that inpingue on the detector.
The main environmental contribution is due to source photons that undergo Compton scattering with the surrounding materials and are deflected with angles greater than about 120 (backscattering). At these
angles, the scattered photons have nearly the energy
Ec reported in eq. 2.3. The effect on the measured spectrum
is that a backscattering peak with its maximum at Ec superimposes to the lower-energy side of
the Compton continuum. As we will discuss in next sections, this is a important
factor to take into account in determining gamma-detectors spectral response
by means of calibration spectra. Other minor environmental contribution may come from
characteristic X-rays generated by photo-electric absorption of source photons
in materials very close to the detectors.
(backscattering). At these
angles, the scattered photons have nearly the energy
Ec reported in eq. 2.3. The effect on the measured spectrum
is that a backscattering peak with its maximum at Ec superimposes to the lower-energy side of
the Compton continuum. As we will discuss in next sections, this is a important
factor to take into account in determining gamma-detectors spectral response
by means of calibration spectra. Other minor environmental contribution may come from
characteristic X-rays generated by photo-electric absorption of source photons
in materials very close to the detectors.
Source set-up effects
In laboratory measurements, source photon interaction (e.g. backscattering) with the encapsulating material of the radioactive sources used to generate monochromatic beams of gamma-rays may cause the production of secondary radiation. If these secondary 'source photons' reach the detector, they can introduce additional distortion of the shape of the recorded spectrum.
Detector energy resolution
The basic components of a scintillator spectrometer include the detector crystal, the light piping system, a PMT, a pre-amplifier, a main amplifier and a single or multichannel analyzer. If all this components had ideal response, i.e. the crystal light yield exactly proportional to the energy deposited by the photon, the PMT response proportional to the crystal light output, the assignment of the signal to a PHA channel performed by the electronics proportional to the PMT pulse amplitude, then the full-energy peak (the photo-peak) of the resulting PHA spectrum of a monochromatic beam would be exactly a delta function. In practice, different factors contribute in worsening the correlation between the energy deposited in the detector and final energy channel assigned to the related signal. The result is the widening of the full-energy peak, escape peak, backscattering peak and all other peaks, the smoothing the Compton edge, etc. This effects are expressed
introducing the concept of the detector energy resolution defined as:
| 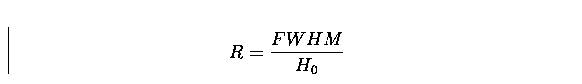 |
(7) |
where FWHM is the Full Width Half Maximum of the full-energy peak and H0
the mean pulse height corresponding to the same peak. An important contribution to energy resolution is due to Poissonian statistical fluctuations of the number of photoelectrons produced in the PMT photocathode for a given crystal light output. In this would be the only energy resolution factor, than the
the full-energy peak would be a Gaussian with FWHM=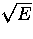 /E0, where E0 is the average energy to produce a photoelectron, and thus R
would be proportional to E-0.5. In practice, there are many other contribution to the finiteness of detector's energy resolution, the main of which are: statistical fluctuations in light production in the crystal, crystal variations in light reflection, crystal internal light absorption, variation of the light collection efficiency as a function of the position in the crystal, non linearity of the crystal light output as a function of electron energy (because of this, the total light output for a given photon energy is different depending on if the energy is converted in kinetic energy of one or more electrons), non uniformity of the photocathode emission, statistical fluctuations in the electron multiplication within the PMT, el;ectronic noise within the pre-amplifier. All these contributions broaden the full-energy peak and
cause the R dependency on energy to deviate from the simple proportionality to E-0.5. Thus, the function R(E) in real detectors is better described as:
/E0, where E0 is the average energy to produce a photoelectron, and thus R
would be proportional to E-0.5. In practice, there are many other contribution to the finiteness of detector's energy resolution, the main of which are: statistical fluctuations in light production in the crystal, crystal variations in light reflection, crystal internal light absorption, variation of the light collection efficiency as a function of the position in the crystal, non linearity of the crystal light output as a function of electron energy (because of this, the total light output for a given photon energy is different depending on if the energy is converted in kinetic energy of one or more electrons), non uniformity of the photocathode emission, statistical fluctuations in the electron multiplication within the PMT, el;ectronic noise within the pre-amplifier. All these contributions broaden the full-energy peak and
cause the R dependency on energy to deviate from the simple proportionality to E-0.5. Thus, the function R(E) in real detectors is better described as:
, where R is usually expressed
in terms of a percentage, as in Tabs. 1.3 and 1.4. Typical values for inorganic
scintillators with an optimal optical coupling, e.g. for NaI, are about 18% at 60 keV and 8-10% at 662 keV; CsI energy resolution is generally a bit worse than that of NaI.
In Fig. 3.4, the main processes contributing to the final measured spectrum of a monochromatic gamma beam are illustrated.
Figure 3.4:
Illustration of various processes contributing to the response of a detector to a gamma-ray source
|




Next: Response matrix and spectral
Up: Gamma-ray spectroscopy with inorganic
Previous: Interaction of gamma radiation
Lorenzo Amati
8/30/1999