The relevant interaction mechanisms of gamma-rays with matter (e.g. [Knoll 1989,Siegbahn 1966]) are photo-electric absorption, Compton scattering and pair production. The relative probability of one of these interactions to occur is a function of the incident photon energy and the atomic number (Z) of the absorbing elements, and is shown in Fig. 3.1.
In photo-electric absorption, all the energy of the incident photon is absorbed by a bound electron of an atom, most likely, for typical gamma-ray energy, a K-shell electron. As a result, a photoelectron is produced, with kinetic energy equal to the initial photon energy minus the shell binding energy. With the loss of an internal electron the atom is left in an excited state from which it relaxes by emitting a characteristic X-ray photon (fluorescence photon) or Auger electrons. The relative probability of fluorescence versus Auger de-excitation is a function of Z and of the interested shell and it is called fluorescence yield ([Dyson 1990,Heitler 1984]). For the K-shell of Cs its value is about 90%. The energy of the Auger electrons ranges from few keV for low-Z materials to tens of keV for atoms with higher atomic number. The atom de-excites with the emission of a characteristic X-ray photon or Auger electrons. If nothing escapes from the detector (the Auger electron has a very short range, due to its low-energy, and the characteristic X-ray photon in CsI has an absorption length of about 1mm), then the whole incident photon energy is deposited in the detector. Thus, the ideal detector (i.e. no photon or electron escape and perfect spectral resolution) spectrum of a monochromatic beam of photons all undergoing photo-electric absorption is a single delta peak at the incident photon energy (Fig. 3.2). The photo-electric cross section goes approximately with the -3 power of photon energy and with the 4th power of atomic number Z.
In the Compton scattering process, incident photons are scattered by
the electrons with a partial energy loss, which depends on the angle ![]() between the directions of the photon before and after the interaction. The energy of the scattered photon,E
between the directions of the photon before and after the interaction. The energy of the scattered photon,E![]() ,
and electron, Ee are given by:
,
and electron, Ee are given by:
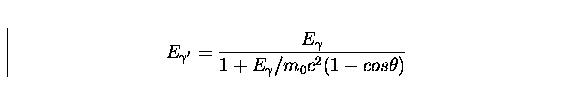 |
(1) |
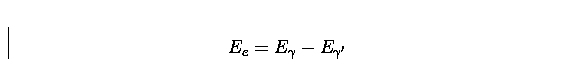 |
(2) |
Thus, the maximum energy Ec deposition occurs when ![]() =180
=180![]() , while for
, while for
![]() close to 0
close to 0![]() nearly all the incident photon energy goes to the
scattered photon and only a small part is converted into electron energy. The resulting
'ideal' spectrum of a monochromatic beam whose photons undergo only Compton scattering is then given by a continuum distribution, which can be calculated from the Klein-Nishina cross section, going from 0 to Ec (called the 'Compton edge'), which is always lower
than the incident photons energy. The gap between the incident photon energy and the Compton edge energy can be calculated with the above formulas with
nearly all the incident photon energy goes to the
scattered photon and only a small part is converted into electron energy. The resulting
'ideal' spectrum of a monochromatic beam whose photons undergo only Compton scattering is then given by a continuum distribution, which can be calculated from the Klein-Nishina cross section, going from 0 to Ec (called the 'Compton edge'), which is always lower
than the incident photons energy. The gap between the incident photon energy and the Compton edge energy can be calculated with the above formulas with ![]() =180
=180![]() :
:
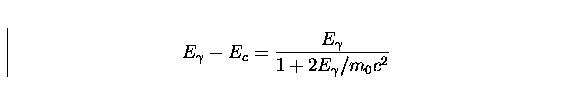 |
(3) |
The probability of Compton scattering is approximately proportional to E and to Z-1.
Finally, pair production can occur if the incident photon has an energy greater than 1.022 MeV (i.e. twice the electron rest energy), consisting in the annihilation of the photon and the creation of an electron-positron pair in the field of a nucleus of the absorbing material. The photon energy in excess to 1.022 MeV is transformed in kinetic energy of the electron and positron. Thus, in ideal conditions, i.e. no electron or positron escape, no positron decay and perfect detector resolution, the spectrum of the monochromatic beam is given by a single delta peak with energy equal to the photon energy minus 1.022 MeV.
The transmitted intensity of a monochromatic gamma-ray beam of photon energy E and intensity I0 crossing an absorbing layer is a function of the photons energy E, the layer
thickness d and the total linear attenuation coefficient as a function of energy, ![]() , of the material constituting the layer, and is given by:
, of the material constituting the layer, and is given by:
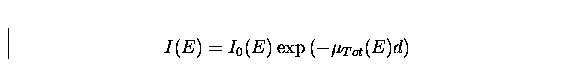 |
(4) |
and the absorbed intensity is given by
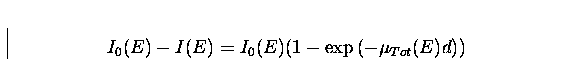 |
(5) |
The linear attenuation coefficient is expressed in cm-1 and is obtained by multiplying the cross section (in cm2/gr) with the absorbing medium density. The total linear attenuation coefficient accounts for absorption due to all the relevant interaction mechanisms:
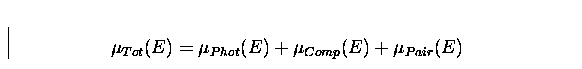 |
(6) |
The total linear coefficient of NaI and CsI as a function of energy and sum of the components due to the three different mechanisms described above are shown in Fig. 3.3.