 |
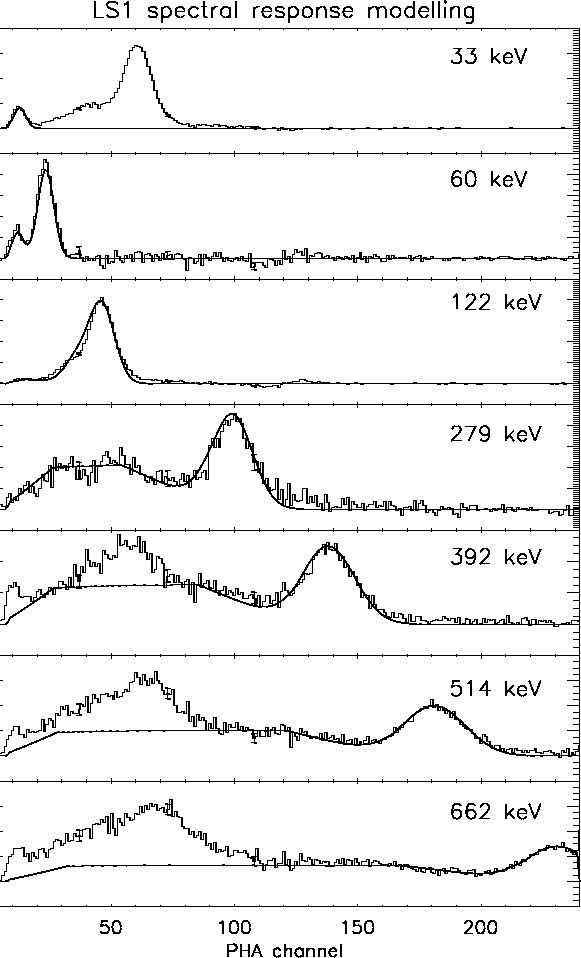
In section 2.4.4 we have shown and discussed the different components of LS1 and LS3 spectra taken during ESTEC calibrations. To reconstruct detectors response functions it was necessary to model each component dependency on energy. The photo-peak component was modeled utilizing the energy resolution relationship and the photo-peak efficiency versus energy. The Compton continuum was modeled as a (semi)rectangular component of area calculated from the ratio of the CsI Compton and photo-electric absorption cross section. To the Compton area we subtracted the counts due to multiple scattering events which fill the gap between photo-peak and the Compton edge (modeled as a Gaussian edge with FWHM equal to the detector resolution at the edge energy) and whose quantity was determined empirically. At low energies, the escape peak was modeled as a Gaussian with FWHM equal to the energy resolution at the escape energy. At these energies the Compton continuum component was assumed to be zero.
The LS1 and LS3 spectra obtained by convolving input line spectra at the calibrations sources energy, and with the same fluxes, with the response matrices are shown in figures 3.18 and 3.19 superimposed to the relative measured data.