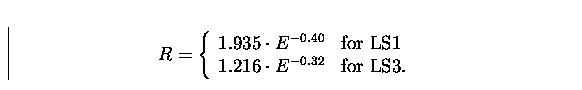next up previous contents
Next: Spectral shape modeling Up: Spectral response matrices of Previous: Spectral response matrices of

Channel to energy conversion and energy resolution

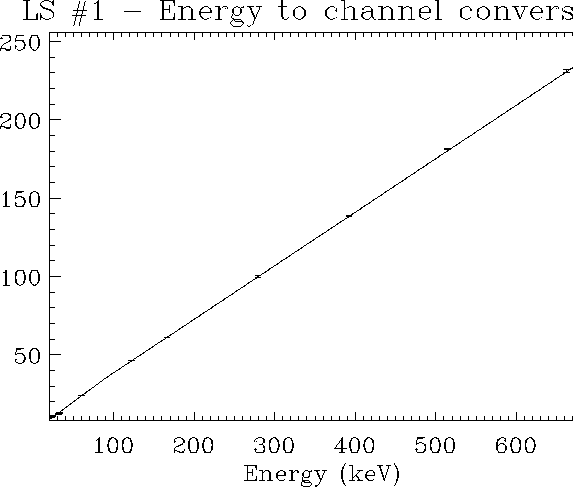
By gauss-fitting the photo-peaks at the various energies, we estimate channel centroid and intensity of the photo-peak. Comparing the estimated source flux with the total measured counts under the peak, we obtain the photo-peak efficiency. In this way we derived the channel and energy resolution vs. energy relationships (figures 3.14, 3.15). The energy to channel relationship shows in both cases a slope change at about 90 keV energy.


  
Figure 3.14: LS1 channel to energy conversion
\begin{figure} \epsfxsize=16cm \centerline{ \epsffile {chan1.ps} }\end{figure}


  
Figure 3.15: LS3 channel to energy conversion
\begin{figure} \epsfxsize=16cm \centerline{ \epsffile {chan3.ps} }\end{figure}

The LS1 and LS3 energy resolution, defined by $R = {\rm FWHM}/H_0$, where H0 is the centroid channel of the photo-peak, as a function of photon energy, is shown in figures 3.16 and 3.17. The best fit function to LS1 and LS3 energy resolution data are given by:

\begin{displaymath} R = \left\{ \begin{array} {ll} 1.935 \cdot E^{-0.40} & \mbo... ...\ 1.216 \cdot E^{-0.32} & \mbox{for LS3.} \end{array} \right.\end{displaymath}


  
Figure 3.16: LS1 Energy resolution.
\begin{figure} \epsfxsize=16cm \centerline{ \epsffile {res1.ps} }\end{figure}


  
Figure 3.17: LS3 Energy resolution.
\begin{figure} \epsfxsize=16cm \centerline{ \epsffile {res3.ps} }\end{figure}

next up previous contents
Next: Spectral shape modeling Up: Spectral response matrices of Previous: Spectral response matrices of
Lorenzo Amati
8/30/1999