Analytical interpolation of LS1 and LS3 efficiency angular dependency

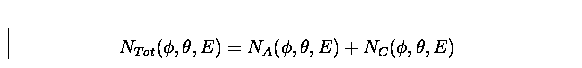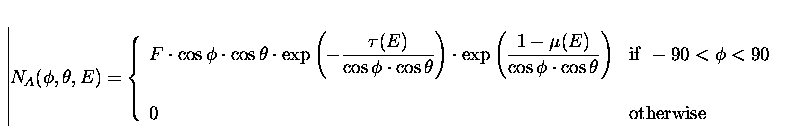
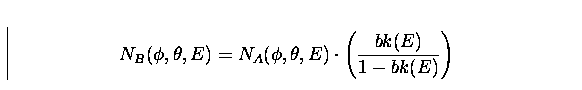
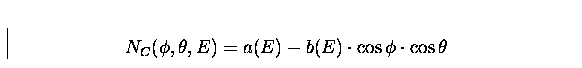
The measured response of LS1 and LS3 with azimuth, elevation and energy of the incident radiation beam was fitted with analytical functions in order to simplify the estimate of the incident fluxes from celestial sources. These functions are also used to compare results of the MC code developed for the GRBM with the calibration tests results. As we discussed in the previous section, the ESTEC calibrations angular light curves of LS1 and LS3 are pretty close to an absorbed (i.e. multiplied by an exponential photon extinction function) cosine. Thus we used an analytical function, based on physical, geometrical and partly empirical considerations, to fit LS1 and LS3 response curves. We described the response function of LS1 and LS3 as the sum of three components:

A)

a component that describes the angular dependency of the projected surface area of the shield on photon direction, the dependency of the transparency of the material in front of the shield on photon direction and the CsI crystal absorption dependency on photon energy and direction:

$$N_A (\phi,\theta,E) = \left\{ \begin{array} {ll} F \cdot \c... ... < \phi < 90 \\ & \\ 0 & {\rm otherwise} \end{array} \right.$$

where F is the direct flux from the radioactive source in photons/cm²/keV; $\tau(E)$ is the average optical depth of the absorbing material in front of the shield, and $\mu(E)$ is the 1 cm thick CsI transparency.

B)

a component that takes into account the environmental back-scattering contribution to the total measured counts:

$$N_{B}(\phi,\theta,E) = N_{A}(\phi,\theta,E) \cdot \left( \frac{bk(E)}{1 - bk(E)} \right)$$

where: $bk(E)\equiv$ (fraction of back-scattering counts)/(total counts).

C)

a semi-empirical component which includes possible side-scattering effects from the satellite structure and PDS subsystems including materials of the lateral shields themselves. These effects are particularly relevant at high energies where we can observe that the counts do not go to zero even when the shield is not directly illuminated by the source. This term is given by:

$$N_{C}(\phi,\theta,E) = a(E) - b(E) \cdot \cos\phi \cdot \cos\theta$$

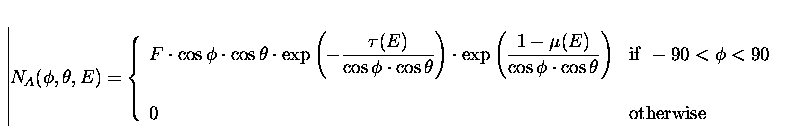
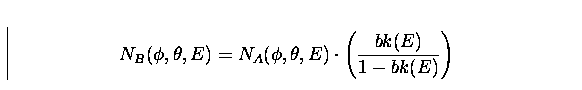
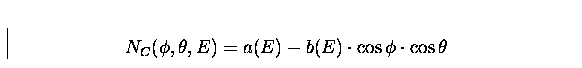
Thus, the total count is given by:

$$N_{Tot}(\phi,\theta,E) = N_{A}(\phi,\theta,E) + N_{B}(\phi,\theta,E) + N_{C}(\phi,\theta,E)$$

with 5 free parameters F, $\tau(E)$, bk(E), a(E) and b(E).

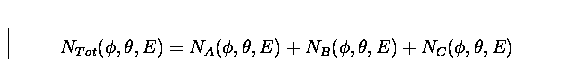
The only deviation of the angular response of LS3 from the above function is a slight change in the slope of the curve at an azimuth angle of about $-60^\circ$. The value of this ``critical'' angle varies of some degrees at the different energies. To reproduce this feature we introduced a change of the optical depth at $-60^\circ$, thus adding one free parameter to the basic function.

The angular response of LS1 is well fit at low energies (60 keV and 122 keV) by the basic function. At higher energies we have a double change in the slope at about $-60^\circ$ (as for LS1) and $+65^\circ$. Thus, we introduced two changes in the optical depth at the critical angles to describe these features. We also applied other minor elevation dependent corrections to the basic form to better describe small features present in negative elevation angles response curves of both LS1 and LS3.

We found good fits ($\chi^{2}$) values lower than 1.2 for 139 d.o.f) of these functions to the data for azimuthal angles between -75$^{\circ}$ and +75$^{\circ}$ and elevation angles between -30$^{\circ}$ and +30$^{\circ}$. Outside these intervals, the angular response curves show features which will be probably better described by MC simulations. Fits results for LS3 at $\theta$=0$\rm ^{\circ}$ are reported in figures from 3.7 to 3.13, where the analytical function is superimposed to the measured data and also fit residuals are plotted.

  

Figure 3.7: Analytical fitting of LS3 azimuthal angular response at 60 keV and $\theta$=0

  

Figure 3.8: Analytical fitting of LS3 azimuthal angular response at 122 keV and $\theta$=0

  

Figure 3.9: Analytical fitting of LS3 azimuthal angular response at 166 keV and $\theta$=0

  

Figure 3.10: Analytical fitting of LS3 azimuthal angular response at 279 keV and $\theta$=0

  

Figure 3.11: Analytical fitting of LS3 azimuthal angular response at 392 keV and $\theta$=0

  

Figure 3.12: Analytical fitting of LS3 azimuthal angular response at 514 keV and $\theta$=0

  

Figure 3.13: Analytical fitting of LS3 azimuthal angular response at 662 keV and $\theta$=0

To estimate in-flight efficiencies we neglect the N_B component that, as discussed above, is mainly due to back-scattering photons from the room walls. Thus, the function describing the in-flight angle-energy dependency of shield efficiency has the form:

$$N_{Tot}(\phi,\theta,E) = N_{A}(\phi,\theta,E) + N_{C}(\phi,\theta,E)$$

with N_A and N_B including the various shield and elevation specific corrections mentioned above.